1. 空間の種別を学ぶ¶
このチュートリアルでは四角格子空間(セル空間)の使い方を学び、コンウェイのライフゲームのモデルをつくります。
ライフゲームとは、セルオートマトンの一種で、1970年に英国の数学者ジョン・コンウェイ(John Conway)が考案しました。
「セルオートマトン(Cellular Automaton)」というのは、空間に格子状に敷き詰められた多数のセルが、 近隣のセルと相互作用をする中で自らの状態を時間的に変化させていく、仮想的な「自動機械(オートマトン)」のことです。ごく抽象的なモデルですが、様々な物理現象や生命現象の本質を表現できるモデルとして、いろいろな種類のセルオートマトンが考案されてきました。
ライフゲームも直接的には生命現象をモデル化するために作られました。
実際、個々のセルが変化する中で実に様々なパターンが空間上に現れるため、それらが生命現象であるかどうかは別にして、単純に見ていて飽きることがありません。 そのため、ライフゲームは、研究者のみならず、様々な人々の興味・関心・趣味の対象となってきました。おそらく最も有名なセルオートマトンと言えるのではないでしょうか。(MASコミュニティ ライフゲームモデルより)

とても有名で興味深いモデルですが、artisoc Cloudを使えば容易に作成することができます。 第3部では以下のようなことを学びながら、最終的には上の動画のようなライフゲームモデルを作成します。
四角格子空間の意味と使い方
同期問題について
それでは内容に取り掛かりましょう。
1.1. 四角格子空間を使う¶
ライフゲームモデルの作成に取り掛かる前に、四角格子空間について学んでいきます。
これまでのチュートリアルでは連続空間を使ってモデルをつくってきました。ここまでのチュートリアルで作成したモデルがある人はモデルを開いて確認してみましょう。空間の種類は空間の設定画面を開き「空間種別」の欄で確認することができます。
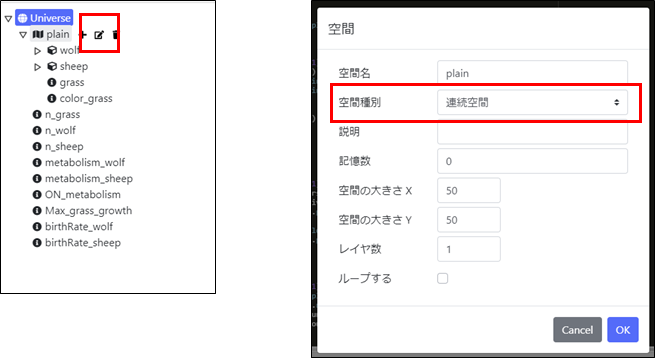
そもそもartisoc Cloudでは空間種別として連続空間か四角格子空間の2種類から選択することができます。この違いを理解するために簡単なモデルを作成してみましょう。
まず、「新規モデルの作成」から新しくモデルの画面を開き、モデルには「教室」と名前を付けましょう。次に、ルール画面を表示し、モデルツリーのUniverseの下に空間を追加します。最初は空間種別を連続空間にしたまま空間を作成します。空間名は「classroom」、空間の大きさは、X=5, Y=5にしておきましょう。「ループする」はチェックを外しておいてください。classroomの下には「student」という名前でエージェントを追加しましょう。
ルールは以下のようにします。
classroomには5人のstudentがランダムな位置にいる
studentはランダムな方向に向かって1ステップに1移動する
ルールは簡単ですのでforward関数を使って自力で書いてみましょう。
ルールが書けたらマップ出力設定をします。マップの選択とエージェントの選択はいつも通り行ってください。マップ要素リストには、「生徒」という名前でstudentを選択します。これまでと違う点として、マップ出力設定画面で罫線表示をチェス型にします。 その他の設定はデフォルトで大丈夫です。
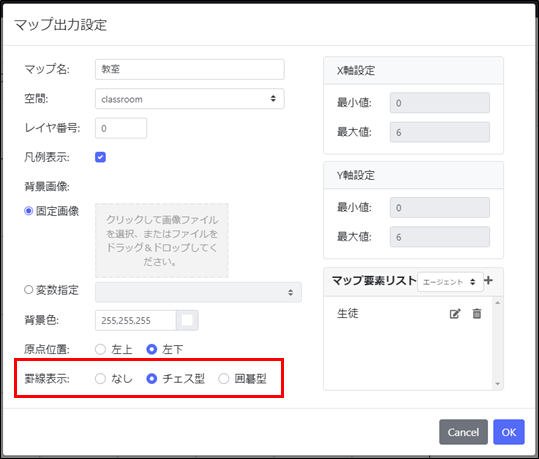
設定ができたらOKを押してください。すると、マップ上に6マス×6マスの罫線が表示されたと思います。(空間の大きさはX=5, Y=5に設定したはずなのにマップは6マス×6マスで表示されたことに違和感を感じた方がいるかもしれませんが、これについては後ほど説明します。)

このマス目を教室の席だと見立てましょう。5人の生徒は席を自由に移動します。
それでは再生してみましょう。今回はステップ実行をしてみます。実行コントロールバーの左から2番目を押してください。このボタンでシミュレーションを1ステップずつ実行することができ、これをステップ実行と呼んでいます。
するとどうでしょう、生徒エージェントはマス目を全く無視して移動してしまいます。
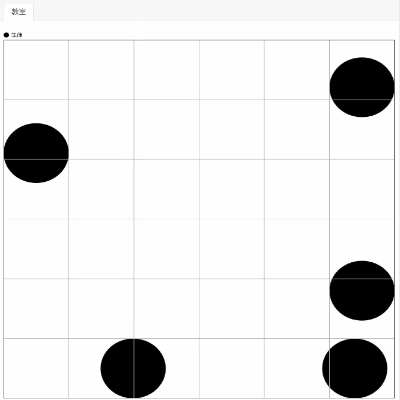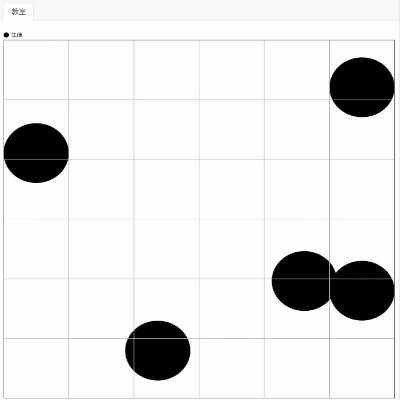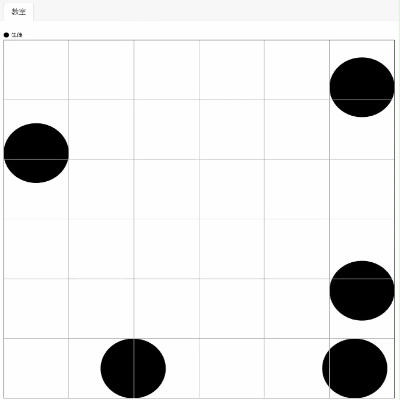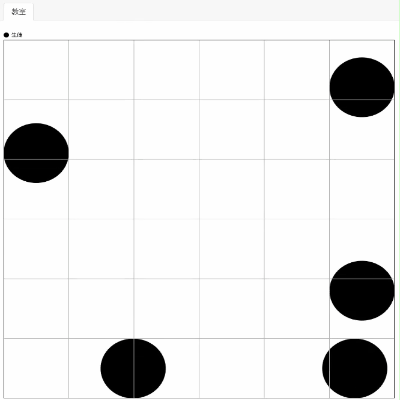
これが連続空間です。連続空間ではエージェントの座標は実数をとります。エージェントの座標が小数をとるとき、マス目を無視して位置してしまうのです。
しかし、生徒たちに正しく席についてもらうためには座標は整数でないと困ります。連続空間上で無理やりそうさせることもできますがもっとシンプルな方法が、四角格子空間の利用です。
ルール画面に戻り、空間classroomの設定画面を開いてください。今度は空間種別を四角格子空間にします。
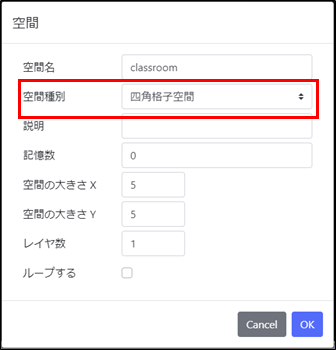
OKを押したら再び実行画面に戻りましょう。マス目が5マス×5マスに変化していると思います。(この理由も後ほど出てきます。)
さて、実行ボタンを押してみてください。すると、シミュレーションは動かず、コンソール画面にエラーが表示されます。
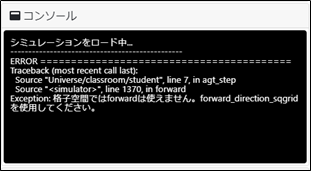
エラー画面ではforward_direction_sqgridを使うように言われますが、今回は目的に合わせてmove_space_around_own_sqgrid関数を使います。
これは四角格子空間専用の便利な関数で、指定した視野の範囲で空き地(格子)を探し、移動します。検索された領域に複数の空き地が存在するときは、ランダムに移動位置を決定します。例えば下記のように書きます。
# 視野1の範囲の格子のうち、エージェントが誰もいない場所へランダムに移動する
self.move_space_around_own_sqgrid(1)
この関数を使えば、生徒を空いている席に移動させることができます。
(初期位置についてはランダムに配置しているので重なってしまうこともありますが、今回は簡単に説明するためこのままにしておきます。 )
では、studentのルールを以下のように書き換えてください。
def agt_init(self):
self.x = 5 * rand()
self.y = 5 * rand()
def agt_step(self):
self.move_space_around_own_sqgrid(1)
それではステップ実行をしてみてください。今度は生徒たちがきちんと格子の中に納まるように移動しました。

このように、四角格子空間ではエージェントの座標は整数しかとりません。そのため、エージェントがとびとびに(離散的に)移動します。
また、四角格子空間用の様々な関数も用意されています。罫線に関しても今回使用したチェス型罫線だけでなく、囲碁のようにエージェントが交点に位置する囲碁型罫線が選択できます。
つくりたいモデルに合わせて空間を選ぶようにしましょう。
ところで、どうして5×5の空間を用意すると連続空間では6マス×6マスの罫線が表示され、四角格子空間では5マス×5マスの罫線が表示されたのでしょうか?
以下ではチェス型の罫線を引いて考えます。
連続空間では、空間の大きさを5×5にした場合、エージェントの取り得る座標の範囲は0 ≤ x < 5, 0 ≤ y < 5です。もしも、マップに表示される罫線が5マス×5マスだった場合にエージェントがx = 4.9, y = 4.9に位置すると、ほとんど、あるいは全くエージェントが見えなくなってしまいます。
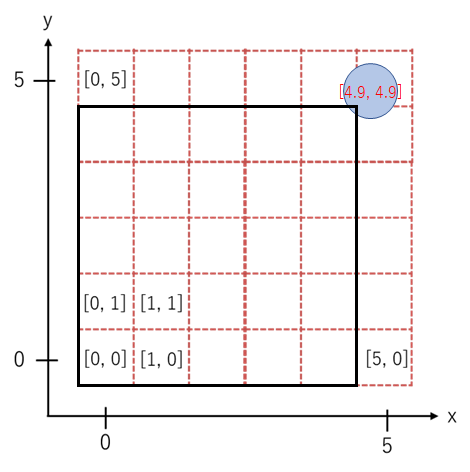
一方、四角格子空間で空間の大きさを5×5にした場合、エージェントの取り得る座標の範囲はx∈{0, 1, 2, 3, 4}, y∈{0, 1, 2, 3, 4}の各5つのみです。よって、最大でも座標はx = 4, y = 4です。この場合は5マス×5マスの表示がちょうどよいということが分かると思います。
1.2. 四角格子空間における「隣のマス」¶
今回はmove_space_around_own_sqgrid関数を使って、視野1の範囲にエージェントを動かしました。この視野1の範囲がどこを指すのかを確認したいと思います。
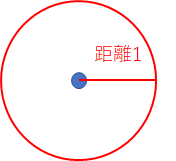
連続空間上で距離1の範囲というと、起点とする座標を中心に描いた半径1の円の範囲になります。つまり、ユークリッド距離で考えます。
一方、四角格子空間における距離の取り方は、一般的に2種類あります。1つ目がチェビシェフ距離、2つ目がマンハッタン距離です。下の図はそれぞれについて、青い丸を起点にしたときの距離を書き込んだ図になります。
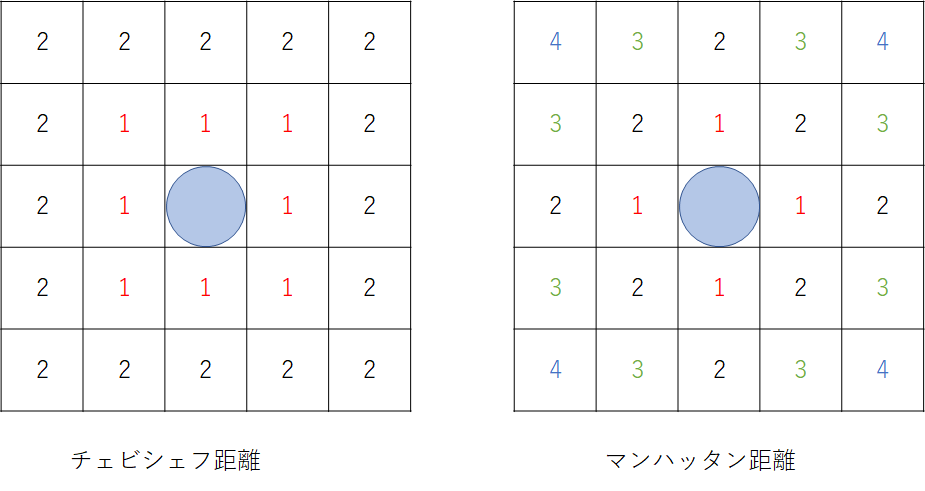
この2つの違いは、斜めのマスの距離をどう捉えるかです。チェビシェフ距離では斜めのマスも距離1、つまり、隣のマスであると考えます。一方、マンハッタン距離は上下左右の4マスのみ隣と考えます。マンハッタン距離では、上下左右のマスにしか進めないというルールで、何マス進めばそのマスに到着するかを考えれば距離がわかります。
artisocではチェビシェフ距離をデフォルトとしています。先ほど書いたルールではmove_space_around_own_sqgrid(1)としていたので、エージェントが次のステップに移動できるマスは上下左右斜めの合計8マスになります。(中央セルとその周囲8マス、計9マスをムーア近傍と呼びます。)
ただし、引数を変えればマンハッタン距離を使うこともできます。move_space_around_own_sqgrid(1, manhattan=True)のように書くと、マンハッタン距離で視野1つまり、上下左右の合計4マスのうち空いているマスにランダムに移動させることができます。(中央セルとその周囲4マス、計5マスをノイマン近傍と呼びます。)
こちらも必要に応じて使い分けてください。
ここでは、四角格子空間について以下のようなことを学びました。
設定の方法
エージェントの座標の取り方
四角格子空間用の関数
距離の取り方
四角格子空間についておおよそ理解できたでしょうか。
1.3. 参考¶
この章のサンプルモデルは次の通りです。